For quasilinear integrodifferential equations of the form

where
 is a scalar singular integral kernel that
behaves like
is a scalar singular integral kernel that
behaves like
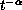 ,
,
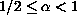 and
and  is integrable over space and time.
is integrable over space and time.
Hans Engler
Abstract:
For quasilinear integrodifferential equations of the form

where
 is a scalar singular integral kernel that
behaves like
is a scalar singular integral kernel that
behaves like
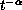 ,
,
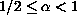 and
and  is integrable over space and time.
is integrable over space and time.
Submitted December 15, 1994. Published February 24, 1995.
Math Subject Classification: 45K05
Key words: Integro-differential equation, strong solution, singular kernel,
quasilinear.
Show me the PDF file (218 KB), TEX file for this article.