We analyze finite time singularity formation for two systems of hyperbolic equations. Our results extend previous proofs of breakdown concerning
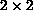 non-strictly hyperbolic systems to
non-strictly hyperbolic systems to
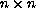 systems, and to a situation where, additionally, the condition of
genuine nonlinearity is violated throughout phase space. The systems
we consider include as special cases those examined by Keyfitz and
Kranzer and by Serre. They take the form
systems, and to a situation where, additionally, the condition of
genuine nonlinearity is violated throughout phase space. The systems
we consider include as special cases those examined by Keyfitz and
Kranzer and by Serre. They take the form

where
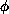 is a scalar-valued function of the n-dimensional
vector
is a scalar-valued function of the n-dimensional
vector
 , and
, and
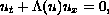
under the assumption
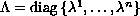 with
with
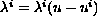 ,
where
,
where
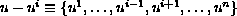 .
.