Existence of positive radially symmetric solutions to a Dirichlet problem of the form
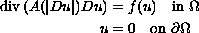
is studied by using blow-up techniques. It is proven here that by choosing the functions
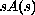 and
and
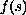 among a certain class called
among a certain class called
Marta Garcia-Huidobro, Raul Manasevich, & Pedro Ubilla
Abstract:
Existence of positive radially symmetric solutions to a
Dirichlet problem of the form
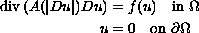
is studied by using blow-up techniques. It is proven here that by
choosing the functions
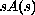 and
and
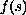 among a certain class called
among a certain class called
Submitted February 12, 1995. Published August 11, 1995.
Math Subject Classification: 35J65.
Key Words: Dirichlet Problem, Positive Solution, Blow up.
Show me the PDF file (226 KB), TEX file for this article.
 |
Marta Garcia-Huidobro Departamento de Matematicas Facultad de Matematica Universidad Catolica de Chile Casilla 306, Correo 22, Santiago, Chile e-mail: mgarcia@poincare.mat.puc.cl |
| Raul Manasevich Departamento de Ingenieria Matematica, F.C.F.M., Universidad de Chile Casilla 170, Correo 3, Santiago, Chile e-mail: manasevi@dim.uchile.cl | |
| Pedro Ubilla Departamento de Matematicas, Universidad de Santiago de Chile Casilla 307, Correo 2, Santiago, Chile e-mail: pubilla@fermat.usach.cl |
Return to the EJDE home page.