We study certain approximate solutions of a system of equations formulated in an earlier paper (Physica D 43, 44-62 (1990)) which in dimensionless form are
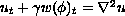 ,
,  ,
,where
 is (dimensionless) temperature,
is (dimensionless) temperature,
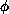 is an order
parameter,
is an order
parameter,
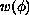 is the temperature-independent part of the energy
density, and
is the temperature-independent part of the energy
density, and
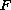 involves the
involves the
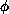 -derivative
of the free-energy density. The constants
-derivative
of the free-energy density. The constants
 and
and
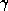 are of
order 1 or smaller, whereas
are of
order 1 or smaller, whereas
 could be as small as 10-8.
Assuming that a solution has two single-phase regions separated
by a moving phase boundary
could be as small as 10-8.
Assuming that a solution has two single-phase regions separated
by a moving phase boundary
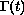 ,
we obtain the differential equations and boundary conditions satisfied by
the `outer'solution valid in the sense of formal asymptotics away from
,
we obtain the differential equations and boundary conditions satisfied by
the `outer'solution valid in the sense of formal asymptotics away from
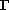 and the
`inner' solution valid close to
and the
`inner' solution valid close to
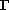 .
Both first and second order transitions are treated.
In the former case, the `outer' solution obeys a free boundary problem for
the heat equations with a Stefan-like condition expressing conservation of
energy at the interface and another condition relating the velocity of the
interface to its curvature, the surface tension and the local
temperature. There are
O(
.
Both first and second order transitions are treated.
In the former case, the `outer' solution obeys a free boundary problem for
the heat equations with a Stefan-like condition expressing conservation of
energy at the interface and another condition relating the velocity of the
interface to its curvature, the surface tension and the local
temperature. There are
O( )
effects not present in the
standard phase-field model, e.g. a correction to the Stefan
condition due to stretching of the interface. For second-order
transitions, the main new effect is a term proportional to the
temperature gradient in the equation for the interfacial velocity. This
effect is related to the dependence of surface tension on temperature.
)
effects not present in the
standard phase-field model, e.g. a correction to the Stefan
condition due to stretching of the interface. For second-order
transitions, the main new effect is a term proportional to the
temperature gradient in the equation for the interfacial velocity. This
effect is related to the dependence of surface tension on temperature. 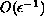 )
within the interface, leading to an extra term in
the Stefan condition proportional (in two dimensions)
to the second derivative of curvature with respect to arc length. In
the other, the order parameter has m components, leading naturally
to anisotropies in the interface conditions.
)
within the interface, leading to an extra term in
the Stefan condition proportional (in two dimensions)
to the second derivative of curvature with respect to arc length. In
the other, the order parameter has m components, leading naturally
to anisotropies in the interface conditions.