Electron. J. Diff. Eqns.,
Vol. 1995(1995), No. 17, pp 1-14.
Reflectionless Boundary Propagation Formulas
for Partial Wave Solutions to the Wave Equation
Jaime Navarro & Henry A. Warchall
Abstract:
We consider solutions to the wave equation in 3+1 spacetime
dimensions whose data is compactly supported at some initial time.
For points outside a ball containing the initial support, we develop an
outgoing wave condition, and associated one-way propagation formula,
for the partial waves in the spherical-harmonic decomposition of the
solution. The propagation formula expresses the
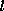 -th partial wave at
time t and radius a in terms of order-l
radial derivatives
of the partial wave at time
-th partial wave at
time t and radius a in terms of order-l
radial derivatives
of the partial wave at time
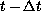 and radius
and radius
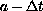 .
The boundary propagation formula can be applied to any differential
equation that is well-approximated by the wave equation outside a
fixed ball.
.
The boundary propagation formula can be applied to any differential
equation that is well-approximated by the wave equation outside a
fixed ball.
Submitted May 20, 1994. Published November 28, 1995.
Math Subject Classification: 35L05, 35L15, 35C10, 35A35, 35A22.
Key Words: One-sided wave propagation, Wave equation, Reflectionless
boundary conditions, Partial waves, Spherical-harmonic
decomposition, Open-space boundary conditions.
Show me the
PDF file (194 KB),
TEX file for this article.
 |
Jaime Navarro
Universidad Autonoma Metropolitana
Unidad Azcapotzalco, Division de Ciencias Basicas
Apdo. Postal 16-306,
Mexico D.F. 02000, Mexico
e-mail: jnfu@hp9000a1.uam.mx
|
 |
Henry A. Warchall
Department of Mathematics,
University of North Texas
Denton TX 76203-5116, USA
e-mail: hankw@unt.edu
|
Return to the EJDE home page.
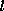 -th partial wave at
time
-th partial wave at
time 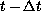 and radius
and radius
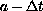 .
The boundary propagation formula can be applied to any differential
equation that is well-approximated by the wave equation outside a
fixed ball.
.
The boundary propagation formula can be applied to any differential
equation that is well-approximated by the wave equation outside a
fixed ball.

