In a previous paper we have considered the functional

subject to

where
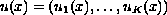 belongs to
belongs to
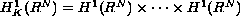
(K times) and
 means
means
 .
. We have shown that, under some technical assumptions and except for a translation in the space variable
In this paper we consider a similar question except that the integrals in the definition of the functionals are taken on some set
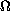 which is
invariant under rotations but not under translations, that is,
which is
invariant under rotations but not under translations, that is,
 is
either a ball, an annulus or the exterior of a ball. In this case we show
that for the minimization problem without constraint, global minimizers
are radially symmetric. However, for the constrained problem, in general,
the minimizers are not radially symmetric. For instance, in the case of
Neumann boundary conditions, even local minimizers are not radially
symmetric (unless they are constant). In any case, we show that the
global minimizers have a symmetry of codimension at most one.
is
either a ball, an annulus or the exterior of a ball. In this case we show
that for the minimization problem without constraint, global minimizers
are radially symmetric. However, for the constrained problem, in general,
the minimizers are not radially symmetric. For instance, in the case of
Neumann boundary conditions, even local minimizers are not radially
symmetric (unless they are constant). In any case, we show that the
global minimizers have a symmetry of codimension at most one.
We use our method to extend a very well known result of Casten and Holland to the case of gradient parabolic systems. The unique continuation principle for elliptic systems plays a crucial role in our method.