Electron. J. Diff. Eqns., Vol. 1997(1997), No. 01, pp 1-12.
Sub-elliptic boundary value problems for quasilinear elliptic
operators
Dian K. Palagachev & Peter R. Popivanov
Abstract:
Classical solvability and uniqueness in the Holder space
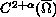 is proved for the oblique derivative problem
is proved for the oblique derivative problem
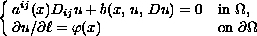
in the case when the vector field
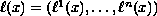 is tangential to the boundary
is tangential to the boundary
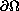 at the points of some
non-empty set
at the points of some
non-empty set
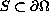 ,
and the nonlinear term
,
and the nonlinear term
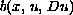 grows quadratically with respect to the gradient
grows quadratically with respect to the gradient
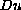 .
.
Submitted October 28, 1996. Published January 8, 1997.
Math Subject Classification: 35J65, 35R25.
Key Words: Quasilinear elliptic operator, degenerate oblique derivative
problem, sub-elliptic estimates.
Show me the
PDF file (216 KB),
TEX and other files for this article.
 |
Dian K. Palagachev
Department of Mathematics
Technological University of Sofia
8 Kl. Okhridski blvd., 1756 Sofia, Bulgaria.
email: dian@bgcict.acad.bg dian@pascal.dm.uniba.it |
| |
Peter R. Popivanov
Institute of Mathematics, Bulgarian Academy of Sciences
G. Bonchev str., bl. 8, 1113 Sofia, Bulgaria
e-mail: popivano@bgearn.acad.bg |
Return to the EJDE home page.
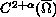 is proved for the oblique derivative problem
is proved for the oblique derivative problem
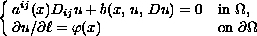
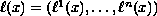 is tangential to the boundary
is tangential to the boundary
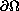 at the points of some
non-empty set
at the points of some
non-empty set
 ,
and the nonlinear term
,
and the nonlinear term
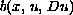 grows quadratically with respect to the gradient
grows quadratically with respect to the gradient
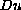 .
.
