We study the role played by the indefinite weight function
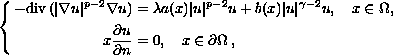
where
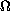 is a smooth bounded domain in
is a smooth bounded domain in
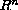 ,
, 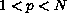 ,
,
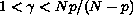 and
and
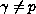 .
We prove that
.
We prove that
Paul A. Binding, Pavel Drabek, & Yin Xi Huang
Abstract:
We study the role played by the indefinite weight
function
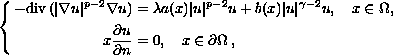
where
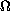 is a smooth bounded domain in
is a smooth bounded domain in
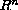 ,
, 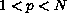 ,
,
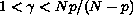 and
and
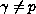 .
We prove that
.
We prove that
 and
and 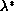 such that
such that
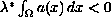 and,
for
and,
for
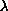 strictly between 0 and
strictly between 0 and
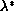 ,
the problem has a positive solution.
,
the problem has a positive solution.
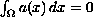 , then the problem has a positive
solution for small
, then the problem has a positive
solution for small
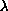 provided that
provided that
 .
.
Submitted September 11, 1996. Published January 30, 1997.
Math Subject Classification: 35J65, 35J70, 35P30.
Key Words: p-Laplacian, positive solutions, Neumann boundary
value problems.
Show me the PDF file (182 KB), TEX file for this article.
| Paul A. Binding Department of Mathematics & Statistics, University of Calgary, Calgary, Alberta, Canada, T2N 1N4 e-mail: binding@acs.ucalgary.ca | |
 |
Pavel Drabek Department of Mathematics University of West Bohemia P.O. Box 314, 30614 Pilsen, Czech Republic e-mail: pdrabek@kma.zcu.cz http://deimos.zcu.cz/Drabek |
| Yin Xi Huang Department of Mathematical Sciences, University of Memphis, Memphis, TN 38152 USA e-mail: huangy@mathsci.msci.memphis.edu |