Electron. J. Diff. Eqns., Vol. 1997(1997), No. 12, pp 1-18.
Behaviour near the boundary for solutions of elasticity systems
V. N. Domingos Cavalcanti
Abstract:
In this article we study the behaviour near the boundary for
weak solutions of the system
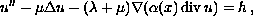
with
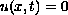 on the boundary of a domain
on the boundary of a domain
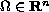 , and
, and
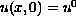 ,
,
 in
in
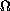 .
We show that the Sobolev norm of the solution in an
.
We show that the Sobolev norm of the solution in an
 -neighbourhood of the boundary can be estimated
independently of
-neighbourhood of the boundary can be estimated
independently of
 .
.
Submitted April 1, 1997. Published July 31, 1997.
Math Subject Classification: 93B05, 93C20, 35B37.
Key Words: Behaviour near the boundary, controllability,
elasticity system
Show me the
PDF file (222 KB),
TEX file for this article.
 |
Valeria N. Domingos Cavalcanti
Universidade Estadual de Maringa,
87020-900 Maringa-PR, Brazil
e-mail: valeria@gauss.dma.uem.br
|
|---|
Return to the EJDE home page
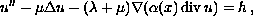
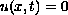 on the boundary of a domain
on the boundary of a domain
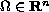 , and
, and
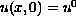 ,
,
 in
in
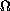 .
We show that the Sobolev norm of the solution in an
.
We show that the Sobolev norm of the solution in an
 -neighbourhood of the boundary can be estimated
independently of
-neighbourhood of the boundary can be estimated
independently of
 .
.
