Electron. J. Diff. Eqns.,
Vol. 1997(1997), No. 22, pp 1-17.
Stable multiple-layer stationary solutions of a semilinear parabolic
equation in two-dimensional domains
Arnaldo Simal do Nascimento
Abstract:
We use
 -convergence to
prove existence of stable multiple-layer
stationary solutions (stable patterns) to the reaction-diffusion equation.
-convergence to
prove existence of stable multiple-layer
stationary solutions (stable patterns) to the reaction-diffusion equation.
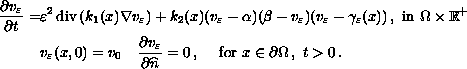
Given nested simple closed curves in
 ,
we give sufficient conditions
on their curvature so that the reaction--diffusion problem possesses
a family of stable patterns.
In particular, we extend to two-dimensional domains and to a spatially
inhomogeneous source term, a previous result by Yanagida and Miyata.
,
we give sufficient conditions
on their curvature so that the reaction--diffusion problem possesses
a family of stable patterns.
In particular, we extend to two-dimensional domains and to a spatially
inhomogeneous source term, a previous result by Yanagida and Miyata.
Submitted May 13, 1997. Published December 1, 1997.
Math Subject Classification: 35K20, 35K57, 35B25.
Key Words: Diffusion equation, Gamma-convergence, transition layers, stable equilibria.
Show me the
PDF file (224 KB),
TEX file for this article.
Arnaldo Simal do Nascimento
Universidade Federal de Sao Carlos, D.M.;
13565-905 - Sao Carlos, S.P. Brazil
e-mail: dasn@power.ufscar.br
Return to the EJDE home page
 -convergence to
prove existence of stable multiple-layer
stationary solutions (stable patterns) to the reaction-diffusion equation.
-convergence to
prove existence of stable multiple-layer
stationary solutions (stable patterns) to the reaction-diffusion equation.
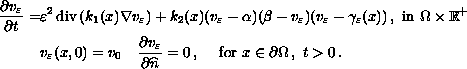
 ,
we give sufficient conditions
on their curvature so that the reaction--diffusion problem possesses
a family of stable patterns.
In particular, we extend to two-dimensional domains and to a spatially
inhomogeneous source term, a previous result by Yanagida and Miyata.
,
we give sufficient conditions
on their curvature so that the reaction--diffusion problem possesses
a family of stable patterns.
In particular, we extend to two-dimensional domains and to a spatially
inhomogeneous source term, a previous result by Yanagida and Miyata.