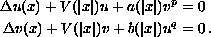Electron. J. Diff. Eqns.,
Vol. 1998(1998), No. 01, pp. 1-27.
Existence of continuous and singular ground states
for semilinear elliptic systems
Cecilia S. Yarur
Abstract:
We study existence results of a curve of continuous and singular
ground states for the system

where
 , the functions f
and g are
increasing Lipschitz continuous functions in
, the functions f
and g are
increasing Lipschitz continuous functions in
 , and
, and
 and
and
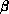 are nonnegative continuous functions in
are nonnegative continuous functions in
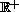 . We also study general systems of the form
. We also study general systems of the form
Submitted September 3, 1997. Published January 16, 1998.
Math Subject Classification: 35J60, 31A35.
Key Words: Semilinear elliptic systems, ground states.
Show me the
PDF file (232 KB),
TEX file for this article.
Cecilia S. Yarur
Departamento de Matematica y C. C.,
Universidad de Santiago de Chile
Casilla 307, Correo 2, Santiago, Chile
e-mail: cyarur@fermat.usach.cl
Return to the EJDE home page

 , the functions f
and g are
increasing Lipschitz continuous functions in
, the functions f
and g are
increasing Lipschitz continuous functions in
 , and
, and
 and
and
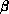 are nonnegative continuous functions in
are nonnegative continuous functions in
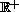 . We also study general systems of the form
. We also study general systems of the form