Electron. J. Diff. Eqns.,
Vol. 1998(1998), No. 11, pp. 1-8.
Barriers on cones for degenerate quasilinear elliptic operators
Michail Borsuk & Dmitriy Portnyagin
Abstract:
Barrier functions
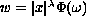 are constructed
for the first boundary value problem as well as for the mixed
boundary value problem for quasilinear elliptic second order
equation of divergent form with triple degeneracy on the
are constructed
for the first boundary value problem as well as for the mixed
boundary value problem for quasilinear elliptic second order
equation of divergent form with triple degeneracy on the
 -dimensional
convex circular cone:
-dimensional
convex circular cone:
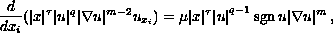
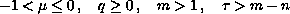 .
.
Submitted May 15, 1997. Published April 17, 1998.
Math Subject Classification: 35J65, 35J70, 35B05, 35B45, 35B65.
Key Words: quasilinear elliptic equations, barrier functions,
conical points.
Show me the
PDF (114K),
TEX file, and other files for this article.
Show me the
PDF file (114 KB),
TEX file, and other files for this article.
Note This article is related to another article published by the EJDE.
Michail Borsuk & Dmitriy Portnyagin,
On the Dirichlet problem for quasilinear elliptic second order
equations with triple degeneracy and singularity in a domain with
a boundary conical point ,
Vol. 1999(1999), No. 23, pp. 1-25.
 |
Michail Borsuk
Department of Applied Mathematics
Olsztyn University of Agriculture and Technology
10-957 Olsztyn-Kortowo, Poland
e-mail: borsuk@art.olsztyn.pl
|
 |
Dmitriy Portnyagin
Department of Physics,
Lvov State University
290602 Lvov, Ukraine |
Return to the EJDE home page
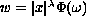 are constructed
for the first boundary value problem as well as for the mixed
boundary value problem for quasilinear elliptic second order
equation of divergent form with triple degeneracy on the
are constructed
for the first boundary value problem as well as for the mixed
boundary value problem for quasilinear elliptic second order
equation of divergent form with triple degeneracy on the
 -dimensional
convex circular cone:
-dimensional
convex circular cone:
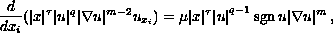
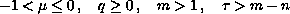 .
.

