Electron. J. Diff. Eqns.,
Vol. 1998(1998), No. 23, pp. 1-8.
Invariance of Poincare-Lyapunov polynomials under the group of rotations
Pierre Joyal
Abstract:
We show that the Poincare-Lyapunov polynomials at a focus of a
family of real polynomial vector fields of degree
 on the plane
are invariant under the group of rotations. Furthermore,
we show that under the multiplicative group
on the plane
are invariant under the group of rotations. Furthermore,
we show that under the multiplicative group
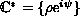 , they are invariant up to a
positive factor. These results follow from the weighted-homogeneity
of the polynomials that we define in the text.
, they are invariant up to a
positive factor. These results follow from the weighted-homogeneity
of the polynomials that we define in the text.
Submitted June 25, 1998. Published October 9, 1998.
Math Subject Classification: 58F14, 58F21, 58F35, 34C25.
Key Words: focus, invariance of Poincare-Lyapunov polynomials,
weighted-homogeneity.
Show me the
PDF file (123 KB),
TEX file for this article.
Pierre Joyal
Departement d'informatique et de mathematique
Universite du Quebec a Chicoutimi
555 boul. de l'Universite, Chicoutimi, G7H 2B1, Canada
e-mail: Pierre_Joyal@uqac.uquebec.caname
Return to the EJDE home page
 on the plane
are invariant under the group of rotations. Furthermore,
we show that under the multiplicative group
on the plane
are invariant under the group of rotations. Furthermore,
we show that under the multiplicative group
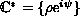 , they are invariant up to a
positive factor. These results follow from the weighted-homogeneity
of the polynomials that we define in the text.
, they are invariant up to a
positive factor. These results follow from the weighted-homogeneity
of the polynomials that we define in the text.