Electron. J. Diff. Eqns.,
Vol. 1998(1998), No. 26, pp. 1-17.
Existence of axisymmetric weak solutions of the 3-D Euler equations
for near-vortex-sheet initial data
Dongho Chae & Oleg Yu Imanuvilov
Abstract:
We study the initial value problem for the 3-D Euler equation when
the fluid is inviscid and incompressible, and flows with
axisymmetry and without swirl.
On the initial vorticity
 ,
we assumed that
,
we assumed that
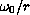 belongs to
belongs to
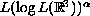 with
with
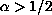 , where
, where
 is the distance
to an axis of symmetry.
To prove the existence of weak global solutions, we prove first
a new a priori estimate for the solution.
is the distance
to an axis of symmetry.
To prove the existence of weak global solutions, we prove first
a new a priori estimate for the solution.
Submitted October 9, 1998. Published October 15, 1998.
Math Subject Classification: 35Q35, 76C05.
Key Words: Euler equations, axisymmetry, weak solution.
Show me the
PDF file (193 KB),
TEX file for this article.
Dongho Chae
Department of Mathematics, Seoul National University
Seoul 151-742, Korea
e-mail: dhchae@math.snu.ac.kr |
Oleg Yu Imanuvilov
Korean Institute for Advanced Study
207-43 Chungryangri-dong Dongdaemoon-ku, Seoul, Korea
e-mail: oleg@kias.kaist.ac.kr |
Return to the EJDE home page
 ,
we assumed that
,
we assumed that
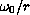 belongs to
belongs to
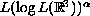 with
with
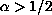 , where
, where
 is the distance
to an axis of symmetry.
To prove the existence of weak global solutions, we prove first
a new a priori estimate for the solution.
is the distance
to an axis of symmetry.
To prove the existence of weak global solutions, we prove first
a new a priori estimate for the solution.