Electron. J. Diff. Eqns.,
Vol. 1998(1998), No. 31, pp. 1-10.
Existence of periodic solutions for a semilinear ordinary differential equation
Petr Girg
Abstract:
Dancer [3] found a necessary and sufficient condition for the existence
of periodic solutions to the equation
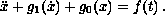
His condition is based on a functional that depends on the solution to
the above equation with
 . However, that solution is not always
explicitly known which makes the condition unverifiable in practical
situations. As an alternative, we find computable bounds for the
functional that provide a sufficient condition and
a necessary condition for the existence of solutions.
. However, that solution is not always
explicitly known which makes the condition unverifiable in practical
situations. As an alternative, we find computable bounds for the
functional that provide a sufficient condition and
a necessary condition for the existence of solutions.
Submitted August 20, 1998. Published November 20, 1998.
Math Subject Classification: 34B15, 34C15, 34C25, 34C99.
Key Words: Ordinary differential equation, periodic solutions.
Show me the
PDF file (138K),
TEX file, and other files for this article.
 |
Petr Girg
Centre of Applied Mathematics,
University of West Bohemia, P.O. Box 314
306 14, Plzen, Czech Republic
e-mail: pgirg@kma.zcu.cz
Web page http://www-cam.zcu.cz/Girg
|
Return to the EJDE web page
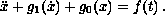
 . However, that solution is not always
explicitly known which makes the condition unverifiable in practical
situations. As an alternative, we find computable bounds for the
functional that provide a sufficient condition and
a necessary condition for the existence of solutions.
. However, that solution is not always
explicitly known which makes the condition unverifiable in practical
situations. As an alternative, we find computable bounds for the
functional that provide a sufficient condition and
a necessary condition for the existence of solutions.