Electron.n. J. Diff. Eqns., Vol. 1999(1999), No. 13, pp. 1-27.
Asymptotic properties of the magnetic integrated density of states
G. D. Raikov
Abstract:
This article could be regarded as a supplement to [11]
where we considered the Schrodinger operator with constant
magnetic field and decaying electric potential, and studied
the asymptotic behaviour of the discrete
spectrum as the coupling constant of the magnetic field tends to infinity.
To describe this behaviour when the kernel of the
magnetic field is not trivial,
we introduced a measure
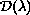 defined on
defined on
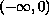 called the ``magnetic integrated density of states''.
In this article, we study the asymptotic behaviour of this measure as
called the ``magnetic integrated density of states''.
In this article, we study the asymptotic behaviour of this measure as
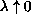 and as
and as
 ,
,
 being the lower bound of the support of
being the lower bound of the support of
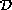 .
.
Submitted October 11, 1998. Published April 26, 1999.
Math Subject Classification: 35J10, 35P20, 81Q10.
Key Words: magnetic Schrodinger operator, integrated density of states,
spectral asymptotics.
Show me the
PDF file (255K),
TEX file for this article.
Georgi D. Raikov
Section of Mathematical Physics
Institute of Mathematics and Informatics
Bulgarian Academy of Sciences
Acad. G. Bonchev Str., bl.8, 1113 Sofia, Bulgaria
e-mail: gdraikov@omega.bg
Return to the EJDE web page
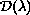 defined on
defined on
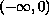 called the ``magnetic integrated density of states''.
In this article, we study the asymptotic behaviour of this measure as
called the ``magnetic integrated density of states''.
In this article, we study the asymptotic behaviour of this measure as
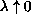 and as
and as
 ,
,
 being the lower bound of the support of
being the lower bound of the support of
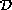 .
.