We study the existence of positive solutions to the boundary-value problem
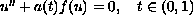
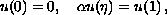
where
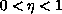 and
and
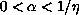 .
We show the existence of at least one positive solution if f is
either superlinear or sublinear by applying the fixed point theorem in cones.
.
We show the existence of at least one positive solution if f is
either superlinear or sublinear by applying the fixed point theorem in cones.
Ruyun Ma
Abstract:
We study the existence of positive solutions to the boundary-value problem
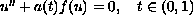
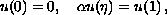
where
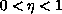 and
and
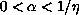 .
We show the existence of at least one positive solution if f is
either superlinear or sublinear by applying the fixed point theorem in cones.
.
We show the existence of at least one positive solution if f is
either superlinear or sublinear by applying the fixed point theorem in cones.
Submitted June 9, 1999. Published September 15, 1999.
Math Subject Classifications: 34B15
Key Words: Second-order multi-point BVP, positive solution, cone, fixed point.
Show me the PDF file (94K), TEX file for this article.
 |
Ruyun Ma Department of Mathematics Northwest Normal University Lanzhou 730070, Gansu, P. R. China e-mail address: mary@nwnu.edu.cn |
Return to the EJDE web page