We prove existence results for the quasilinear elliptic system
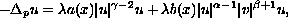
 ,
,where
 and
and
 may reach the
critical Sobolev exponents, and the coefficient functions
may reach the
critical Sobolev exponents, and the coefficient functions 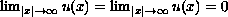 .
.
N. M. Stavrakakis & N. B. Zographopoulos
Abstract:
We prove existence results for the quasilinear elliptic system
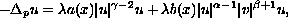
 ,
,
where
 and
and
 may reach the
critical Sobolev exponents, and the coefficient functions
may reach the
critical Sobolev exponents, and the coefficient functions 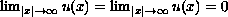 .
.
An addendum was attached on November 4, 2003. The results concerning the critical Sobolev exponent are false; other results still hold. See last page of this article.
Submitted July 16, 1999. Published October 4, 1999.
Math Subject Classifications: 35P30, 35J70, 35B45, 35B65.
Key Words: p-Laplacian, nonlinear eigenvalue problems,
homogeneous Sobolev spaces, maximum principle, Palais-Smale Condition.
Show me the PDF file (179K), TEX file, and other files for this article.