Electron. J. Diff. Eqns., Vol. 1999(1999), No. 42, pp. 1-12.
Infinitely many homoclinic orbits for
Hamiltonian systems with group symmetries
Cheng Lee
Abstract:
This paper deals via variational methods with the existence of infinitely
many homoclinic orbits for a class of the first-order time-dependent
Hamiltonian systems
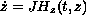
without any periodicity assumption on
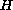 , providing that
, providing that
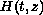 is
G-symmetric with respect to
is
G-symmetric with respect to
 ,
is superquadratic as
,
is superquadratic as
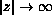 ,
and satisfies some additional assumptions.
,
and satisfies some additional assumptions.
Submitted March 19, 1999. Published October 12, 1999.
Math Subject Classifications: 34B30, 34C37.
Key Words: Hamiltonian system, homoclinic orbits.
Show me the
PDF file (153K),
TEX file, and other files for this article.
Cheng Lee
Department of Mathematics
National Changhua University of Education
Changhua, Taiwan. 50058 R.O.C.
e-mail address: clee@math.ncue.edu.tw
Return to the EJDE web page
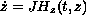
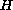 , providing that
, providing that
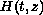 is
G-symmetric with respect to
is
G-symmetric with respect to
 ,
is superquadratic as
,
is superquadratic as
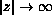 ,
and satisfies some additional assumptions.
,
and satisfies some additional assumptions.