We investigate the exact number of positive solutions of the semilinear Dirichlet boundary value problem
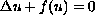
on a ball in
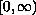 .
For the one-dimensional case we classify all strictly convex
.
For the one-dimensional case we classify all strictly convex
J. Karatson & P. L. Simon
Abstract:
We investigate the exact number of positive solutions of the semilinear
Dirichlet boundary value problem
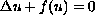
on a ball in 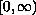 .
For the one-dimensional case we classify all strictly convex
.
For the one-dimensional case we classify all strictly convex
Submitted June 22, 1999. Published October 18, 1999.
Math Subject Classifications: 35J60.
Key Words: semilinear elliptic equations, time-map, bifurcation diagram.
Show me the PDF file (174K), TEX file, and other files for this article.
 |
Janos Karatson Department of Applied Analysis Eotvos Lorand University Budapest, Hungary e-mail: karatson@cs.elte.hu |
 |
Peter L. Simon Department of Applied Analysis Eotvos Lorand University Budapest, Hungary e-mail: simonp@cs.elte.hu |
Return to the EJDE web page