In the noncompact interval
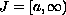 we consider a linear
problem of the form Lx=y,
we consider a linear
problem of the form Lx=y,
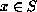 ,
where L is a first order
differential operator, y a locally summable function in
J, and S a subspace of the Frechet space of the
locally absolutely continuous functions in J.
In the general case, the restriction of
L to S is not a Fredholm operator. However,
we show that, under suitable assumptions, S and L(S)
can be regarded as subspaces of
two quite natural spaces in such a way that L becomes a Fredholm
operator between them. Then, the solvability of the problem will be
reduced to the task of finding linear functionals defined in a
convenient subspace of
,
where L is a first order
differential operator, y a locally summable function in
J, and S a subspace of the Frechet space of the
locally absolutely continuous functions in J.
In the general case, the restriction of
L to S is not a Fredholm operator. However,
we show that, under suitable assumptions, S and L(S)
can be regarded as subspaces of
two quite natural spaces in such a way that L becomes a Fredholm
operator between them. Then, the solvability of the problem will be
reduced to the task of finding linear functionals defined in a
convenient subspace of
 whose
``kernel intersection'' coincides with L(S). We will prove that,
for a large class of ``boundary sets'' S, such functionals can
be obtained by reducing the analysis to the case when the function
y has compact
support. Moreover, by adding a suitable stronger
topological assumption on S, the functionals can be represented
in an integral form. Some examples illustrating our results are
given as well.
whose
``kernel intersection'' coincides with L(S). We will prove that,
for a large class of ``boundary sets'' S, such functionals can
be obtained by reducing the analysis to the case when the function
y has compact
support. Moreover, by adding a suitable stronger
topological assumption on S, the functionals can be represented
in an integral form. Some examples illustrating our results are
given as well.



