Electron. J. Diff. Eqns.,
Vol. 2000(2000), No. 01, pp. 1-26.
Exact multiplicity results for quasilinear boundary-value problems
with cubic-like nonlinearities
Idris Addou
Abstract:
We consider the boundary-value problem
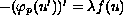 in (0,1)
in (0,1)
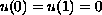
where p> 1,
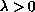 and
and
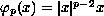 .
The nonlinearity f is cubic-like with three distinct roots
0=a < b< c.
By means of a quadrature method, we provide the exact number of solutions
for all
.
The nonlinearity f is cubic-like with three distinct roots
0=a < b< c.
By means of a quadrature method, we provide the exact number of solutions
for all
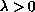 .
This way we extend a recent result, for p=2, by
Korman et al. [17] to the general case p>1. We shall
prove that when
.
This way we extend a recent result, for p=2, by
Korman et al. [17] to the general case p>1. We shall
prove that when
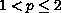 the structure of the solution set is exactly the
same as that studied in the case p=2 by Korman et al.
[17], and strictly different in the case p>2.
the structure of the solution set is exactly the
same as that studied in the case p=2 by Korman et al.
[17], and strictly different in the case p>2.
An addendum was attached on May 3, 2000. There it is shown that
Possibility B of Theorem 2.4 and Possibility D of Theorem 2.5 never happens.
See last page of this article.
Submitted May 26, 1999. Revised October 1, 1999. Published January 1, 2000.
Math Subject Classifications: 34B15.
Key Words: One dimensional p-Laplacian, multiplicity results, time-maps.
Show me the
PDF file (119K),
TEX file for this article.
 |
Idris Addou
USTHB, Institut de Mathematiques
El-Alia, B.P. no. 32 Bab-Ezzouar
16111, Alger, Algerie.
e-mail: idrisaddou@hotmail.com |
Return to the EJDE web page
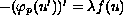 in (0,1)
in (0,1) 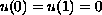
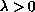 and
and
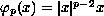 .
The nonlinearity f is cubic-like with three distinct roots
0=a < b< c.
By means of a quadrature method, we provide the exact number of solutions
for all
.
The nonlinearity f is cubic-like with three distinct roots
0=a < b< c.
By means of a quadrature method, we provide the exact number of solutions
for all
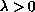 .
This way we extend a recent result, for p=2, by
Korman et al. [17] to the general case p>1. We shall
prove that when
.
This way we extend a recent result, for p=2, by
Korman et al. [17] to the general case p>1. We shall
prove that when
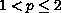 the structure of the solution set is exactly the
same as that studied in the case p=2 by Korman et al.
[17], and strictly different in the case p>2.
the structure of the solution set is exactly the
same as that studied in the case p=2 by Korman et al.
[17], and strictly different in the case p>2. 