 convergence of minimizers of a Ginzburg-Landau functional
convergence of minimizers of a Ginzburg-Landau functional
 convergence of minimizers of a Ginzburg-Landau functional
convergence of minimizers of a Ginzburg-Landau functional
Yutian Lei & Zhuoqun Wu
Abstract:
In this article we study the minimizers of the functional
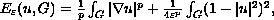
on the class
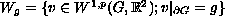 ,
,
where
 is a smooth map with Brouwer degree zero, and
is a smooth map with Brouwer degree zero, and
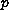 is greater than 2.
In particular, we show that the minimizer converges to the p-harmonic map in
is greater than 2.
In particular, we show that the minimizer converges to the p-harmonic map in
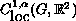 as
as
 approaches zero.
approaches zero.
Submitted September 2, 1999. Published February 21, 2000.
Math Subject Classifications: 35J70.
Key Words: Ginzburg-Landau functional, regularizable minimizer.
Show me the PDF file (193K), TEX file, and other files for this article.