Electron. J. Diff. Eqns., Vol. 2000(2000), No. 18, pp. 1-9.
Minimax principles for critical-point theory in applications
to quasilinear boundary-value problems
A. R. El Amrouss & M. Moussaoui
Abstract:
Using the variational method developed by the same author in [7], we
establish the existence of solutions to the equation
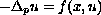 with Dirichlet boundary conditions. Here
with Dirichlet boundary conditions. Here
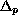 denotes the p-Laplacian and
denotes the p-Laplacian and
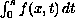 is assumed to lie between the first two eigenvalues of the p-Laplacian.
is assumed to lie between the first two eigenvalues of the p-Laplacian.
Submitted September 9, 1999. Published March 8, 2000.
Math Subject Classifications: 49J35, 35J65, 35B34.
Key Words: Minimax methods, p-Laplacian, resonance.
Show me the
PDF file (134K),
TEX file, and other files for this article.
A. R. El Amrouss & M. Moussaoui
University Mohamed I
Faculty of sciences
Department of Mathematics
Oujda, Moroco
e-mail: amrouss@sciences.univ-oujda.ac.ma
e-mail: moussaoui@sciences.univ-oujda.ac.ma
Return to the EJDE web page
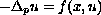 with Dirichlet boundary conditions. Here
with Dirichlet boundary conditions. Here
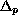 denotes the p-Laplacian and
denotes the p-Laplacian and
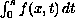 is assumed to lie between the first two eigenvalues of the p-Laplacian.
is assumed to lie between the first two eigenvalues of the p-Laplacian.