Let
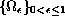 be an indexed family of connected open sets in
be an indexed family of connected open sets in
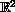 ,
that shrinks to a tree
,
that shrinks to a tree
 as
as
 approaches zero. Let
approaches zero. Let
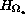 be the Neumann Laplacian and
be the Neumann Laplacian and
 be the restriction of an
be the restriction of an
 function to
function to
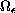 .
For
.
For
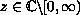 , set
, set
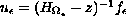 .
Under the assumption that all the edges of
.
Under the assumption that all the edges of
 are line
segments, and some additional conditions on
are line
segments, and some additional conditions on
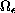 ,
we show that the limit function
,
we show that the limit function
 satisfies a second-order ordinary differential equation on
satisfies a second-order ordinary differential equation on
 with
Kirchhoff boundary conditions on each vertex of
with
Kirchhoff boundary conditions on each vertex of
 .
.