We consider the equation
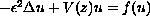 which arises in the study of nonlinear Schrodinger equations.
We seek solutions that are positive on
which arises in the study of nonlinear Schrodinger equations.
We seek solutions that are positive on
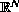 and that vanish at infinity. Under the assumption that f
satisfies super-linear and sub-critical growth conditions,
we show that for small
and that vanish at infinity. Under the assumption that f
satisfies super-linear and sub-critical growth conditions,
we show that for small
 there exist solutions that concentrate
near local minima of V. The local minima may occur in
unbounded components, as long as the Laplacian of V achieves a strict
local minimum along such a component. Our proofs employ
variational mountain-pass and concentration compactness arguments.
A penalization technique developed by Felmer and del Pino is used
to handle the lack of compactness and the absence of the
Palais-Smale condition in the variational framework.
there exist solutions that concentrate
near local minima of V. The local minima may occur in
unbounded components, as long as the Laplacian of V achieves a strict
local minimum along such a component. Our proofs employ
variational mountain-pass and concentration compactness arguments.
A penalization technique developed by Felmer and del Pino is used
to handle the lack of compactness and the absence of the
Palais-Smale condition in the variational framework. 