Electron. J. Diff. Eqns., Vol. 2000(2000), No. 56, pp. 1-18.

Uniqueness of rapidly oscillating periodic solutions to a singularly perturbed differential-delay equation

Hari P. Krishnan

Abstract:
In this paper, we prove a uniqueness theorem for rapidly oscillating periodic solutions of the singularly perturbed differential-delay equation
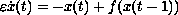$\varepsilon \dot{x}(t)=-x(t)+f(x(t-1))$.
In particular, we show that, for a given oscillation rate, there exists exactly one periodic solution to the above equation. Our proof relies upon a generalization of Lin's method, and is valid under generic conditions.

Submitted December 1, 1999. Published July 24, 2000.
Math Subject Classifications: 34K26, 37G10.
Key Words: delay equation, rapidly oscillating, singularly perturbed.

Show me the PDF file (204K), TEX file for this article.

Hari P. Krishnan
1350 No. Wells St., Apt. D103,
Chicago, IL 60610 USA
e-mail: hkri66@cbot.com, hpk4@columbia.edu
Return to the EJDE web page