Electron. J. Diff. Eqns., Vol. 2000(2000), No. 61, pp. 1-15

Quantitative uniqueness and vortex degree estimates for solutions of the Ginzburg-Landau equation

Igor Kukavica

Abstract:
In this paper, we provide a sharp upper bound for the maximal order of vanishing for non-minimizing solutions of the Ginzburg-Landau equation
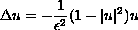
$$ \Delta u=-{1\over\epsilon^2}(1-|u|^2)u $$
which improves our previous result [12]. An application of this result is a sharp upper bound for the degree of any vortex. We treat Dirichlet (homogeneous and non-homogeneous) as well as Neumann boundary conditions.

Submitted June 23, 2000. Published October 2, 2000.
Math Subject Classifications: 35B05, 35J25, 35J60, 35J65, 35Q35.
Key Words: Unique continuation, vortices, Ginzburg-Landau equation.

Show me the PDF file (163K), TEX file, and other files for this article.

Igor Kukavica
Department of Mathematics
University of Southern California
Los Angeles, CA 90089
e-mail: kukavica@math.usc.edu

Return to the EJDE web page