Electron. J. Diff. Eqns., Vol. 2000(2000), No. 66, pp. 1-34.
Exactness results for generalized Ambrosetti-Brezis-Cerami problem and
related one-dimensional elliptic equations
I. Addou, A. Benmezai, S. M. Bouguima , & M. Derhab
Abstract:
We consider the boundary-value problem
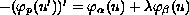 in (0, 1)
in (0, 1)
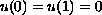 ,
,
where
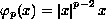 ,
,
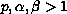 and
and
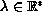 . We give the exact number of
solutions for all
. We give the exact number of
solutions for all
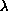 and most
values of
and most
values of 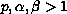 .
In the particular case where
.
In the particular case where
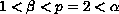 ,
we resolve completely a problem suggested
by A. Ambrosetti, H. Brezis and G. Cerami and which was partially
solved by S. Villegas.
,
we resolve completely a problem suggested
by A. Ambrosetti, H. Brezis and G. Cerami and which was partially
solved by S. Villegas.
Submitted January 1, 2000. Published November 2, 2000.
Math Subject Classifications: 34B15, 34B18.
Key Words: Exactness, p-Laplacian, concave-convex nonlinearities,
quadrature method.
Show me the
PDF file (265K),
TEX file for this article.
 |
Idris Addou
119-8230, Rue Sherbrooke Est,
Montreal, Quebec, H1L-1A9, Canada
email: idrisaddou@yahoo.com |
|
Abdelhamid Benmezai
U.S.T.H.B.-Institut de Mathematiques
El-Alia, BP 32, Bab-Ezzouar
16111, Alger, Algeria
email: abenmzai@hotmail.com |
 |
Sidi Mohammed Bouguima
Department of Mathematics, Faculty of sciences
University of Tlemcen
B.P.119, Tlemcen 13000, Algeria
email: bouguima@yahoo.fr |
|---|
|
Mohammed Derhab
Institut des Sciences Exactes,
Universite Djilali Liabes
BP. 89, Sidi Bel Abbes
22000, Algeria
email: derhab@yahoo.fr |
Return to the EJDE web page
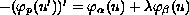 in (0, 1)
in (0, 1) 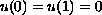 ,
, 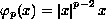 ,
,
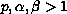 and
and
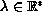 . We give the exact number of
solutions for all
. We give the exact number of
solutions for all
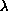 and most
values of
and most
values of 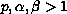 .
In the particular case where
.
In the particular case where
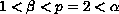 ,
we resolve completely a problem suggested
by A. Ambrosetti, H. Brezis and G. Cerami and which was partially
solved by S. Villegas.
,
we resolve completely a problem suggested
by A. Ambrosetti, H. Brezis and G. Cerami and which was partially
solved by S. Villegas.

