In this paper we study the existence of concentrated solutions of the nonlinear field equation
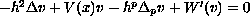 ,
, where
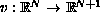 ,
,
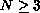 ,
,
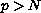 , the
potential
, the
potential
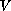 is positive and radial, and
is positive and radial, and
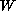 is an appropriate singular
function satisfying a suitable symmetric property.
Provided that
is an appropriate singular
function satisfying a suitable symmetric property.
Provided that
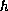 is sufficiently small, we are able to find solutions
with a certain spherical symmetry which exhibit a
concentration behaviour near a circle centered at zero as
is sufficiently small, we are able to find solutions
with a certain spherical symmetry which exhibit a
concentration behaviour near a circle centered at zero as
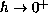 .
Such solutions are obtained as critical points
for the associated energy functional; the proofs of the results are
variational and the arguments rely on topological tools.
Furthermore a penalization-type method is developed for the identification
of the desired solutions.
.
Such solutions are obtained as critical points
for the associated energy functional; the proofs of the results are
variational and the arguments rely on topological tools.
Furthermore a penalization-type method is developed for the identification
of the desired solutions. 