This article collects recent results concerning the behavior at resonance of forced oscillators driven by an asymmetric restoring force, with or without damping. This synthesis emphasizes the key role played by a function denoted by
,
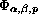which is, up to a sign reversal of its argument,
a correlation product of the forcing term
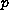and of a function
representing a free oscillation for theundamped equation.
The theoretical results are accompanied by graphical representations
illustrating the behavior of the damped and undamped oscillators.
In particular, the damped oscillator is considered, with a forcing
term whose frequency is close to the frequency of the free oscillations.
For that problem, frequency-response curves are studied, both
theoretically and through numerical computations, revealing a
hysteresis phenomenon, when
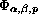is of constant sign.
