Electron. J. Diff. Eqns., Vol. 2001(2001), No. 02, pp. 1-7.
A stability result for p-harmonic systems with discontinuous coefficients
Bianca Stroffolini
Abstract:
The present paper is concerned with p-harmonic systems

where
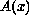 is a positive definite matrix whose entries have
bounded mean oscillation (BMO),
is a positive definite matrix whose entries have
bounded mean oscillation (BMO),
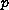 is a real number greater than 1 and
is a real number greater than 1 and
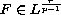 is a given matrix field.
We find a-priori estimates for a very weak solution of class
is a given matrix field.
We find a-priori estimates for a very weak solution of class
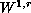 ,
provided
,
provided
 is close to
is close to
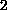 , depending on the BMO norm of
, depending on the BMO norm of
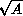 , and
, and
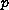 close to
close to
 .
This result is achieved using the corresponding existence and
uniqueness result for linear systems with BMO coefficients
[St], combined with nonlinear commutators.
.
This result is achieved using the corresponding existence and
uniqueness result for linear systems with BMO coefficients
[St], combined with nonlinear commutators.
Submitted November 27, 2000. Published January 2, 2001.
Math Subject Classifications: 35J60, 47B47.
Key Words: Bounded mean oscillation, Linear and Nonlinear Commutators,
Hodge Decomposition.
Show me the
PDF file (117K),
TEX file for this article.
 |
Bianca Stroffolini
Dipartimento di Matematica e Applicazioni
"R. Caccioppoli"
via Cintia, 80126 Napoli, Italy
e-mail: stroffol@matna2.dma.unina.it |
|---|
Return to the EJDE web page

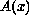 is a positive definite matrix whose entries have
bounded mean oscillation (BMO),
is a positive definite matrix whose entries have
bounded mean oscillation (BMO),
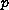 is a real number greater than 1 and
is a real number greater than 1 and
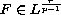 is a given matrix field.
We find a-priori estimates for a very weak solution of class
is a given matrix field.
We find a-priori estimates for a very weak solution of class
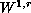 ,
provided
,
provided
 is close to
is close to
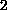 , depending on the BMO norm of
, depending on the BMO norm of
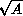 , and
, and
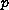 close to
close to
 .
This result is achieved using the corresponding existence and
uniqueness result for linear systems with BMO coefficients
[St], combined with nonlinear commutators.
.
This result is achieved using the corresponding existence and
uniqueness result for linear systems with BMO coefficients
[St], combined with nonlinear commutators. 