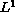 stability of conservation laws for a traffic flow model
stability of conservation laws for a traffic flow model 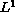 stability of conservation laws for a traffic flow model
stability of conservation laws for a traffic flow model
Tong Li
Abstract:
We establish the
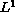 well-posedness theory
for a system of nonlinear hyperbolic
conservation laws with relaxation arising in traffic flows.
In particular, we obtain the continuous dependence
of the solution on its initial data in
well-posedness theory
for a system of nonlinear hyperbolic
conservation laws with relaxation arising in traffic flows.
In particular, we obtain the continuous dependence
of the solution on its initial data in
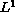 topology.
We construct a functional
for two solutions which is equivalent to the
topology.
We construct a functional
for two solutions which is equivalent to the
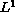 distance
between the solutions. We prove that the functional
decreases in time which yields the
distance
between the solutions. We prove that the functional
decreases in time which yields the
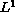 well-posedness of the Cauchy
problem.
We thus obtain the
well-posedness of the Cauchy
problem.
We thus obtain the
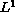 -convergence
to and the uniqueness of
the zero relaxation limit.
We then study the large-time behavior of the entropy solutions.
We show that the equilibrium shock waves are nonlinearly stable in
-convergence
to and the uniqueness of
the zero relaxation limit.
We then study the large-time behavior of the entropy solutions.
We show that the equilibrium shock waves are nonlinearly stable in
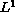 norm. That is, the entropy solution with initial data as certain
norm. That is, the entropy solution with initial data as certain
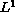 -bounded
perturbations of an equilibrium shock wave exists globally and
tends to a shifted equilibrium shock wave in
-bounded
perturbations of an equilibrium shock wave exists globally and
tends to a shifted equilibrium shock wave in
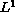 norm as
norm as
 .
We also show that if the initial data
.
We also show that if the initial data
 is bounded and of compact
support,
the entropy solution converges in
is bounded and of compact
support,
the entropy solution converges in
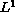 to an equilibrium
to an equilibrium
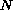 -wave as
-wave as
 .
.
Submitted June 2, 2000. Published February 20, 2001.
Math Subject Classifications: 5L65, 35B40, 35B50, 76L05, 76J10.
Key Words: Relaxation, shock, rarefaction, L^1-contraction,
traffic flows, anisotropic, equilibrium, marginally stable,
zero relaxation limit, large-time behavior, L^1-stability.
Show me the PDF file (277K), TEX file for this article.