Electron. J. Diff. Eqns., Vol. 2001(2001), No. 49, pp. 1-4.
Note on the uniqueness of a global positive solution to the second
Painleve equation
Mohammed Guedda
Abstract:
The purpose of this note is to study the uniqueness of solutions to
 , for
, for
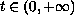
with Neumann condition at 0.
Assuming a certain conditon at infinity,
Helfer and Weissler [6] have found a unique solution.
We show that, without any assumptions at infinity,
this problem has exactly one global positive solution.
Moreover, the solution behaves like
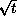 as
as
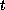 approaches infinity.
approaches infinity.
Submitted February 08, 2001. Published July 9, 2001.
Math Subject Classifications: 34B15, 35B05, 82D55.
Key Words: Second Painleve equation, Neumann condition, global existence.
Show me the
PDF file (190K),
TEX file for this article.
 |
Mohammed Guedda
Universite de Picardie Jules Verne
Faculte de Mathematiques et d'Informatique
33, rue Saint-Leu 80039 Amiens, France
e-mail: Guedda@u-picardie.fr |
|---|
Return to the EJDE web page
 , for
, for
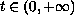
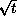 as
as
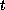 approaches infinity.
approaches infinity.
