Electron. J. Diff. Eqns., Vol. 2001(2001), No. 60, pp. 1-20.

Solutions of nonlinear parabolic equations without growth restrictions on the data

Lucio Boccardo, Thierry Gallouet, & Juan Luis Vazquez

Abstract:
The purpose of this paper is to prove the existence of solutions for certain types of nonlinear parabolic partial differential equations posed in the whole space, when the data are assumed to be merely locally integrable functions, without any control of their behaviour at infinity. A simple representative example of such an equation is
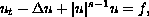
$$ u_t-\Delta u + |u|^{s-1}u=f, $$
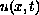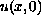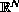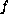which admits a unique globally defined weak solution $u(x,t)$ if the initial function $u(x,0)$ is a locally integrable function in $\mathbb{R}^N$, $N\geq 1$, and the second member $f$ is a locally integrable function of 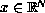$x\in\mathbb{R}^N$ and $t\in [0,T]$ whenever the exponent $s$ is larger than 1. The results extend to parabolic equations results obtained by Brezis and by the authors for elliptic equations. They have no equivalent for linear or sub-linear zero-order nonlinearities.

Submitted July 17, 2001. Published September 12, 2001.
Math Subject Classifications: 35K55, 35K65.
Key Words: Nonlinear parabolic equations, global existence, growth conditions.

Show me the PDF file (413K), TEX file, and other files for this article.

Lucio Boccardo
Dipartimento di Matematica, Universita di Roma 1
Piazza A. Moro 2, 00185
Roma, Italy
e-mail: boccardo@mat.uniroma1.it
Thierry Gallouet
CMI, Universite de Marseille I
13453, France
e-mail: gallouet@cmi.univ-mrs.fr
Juan Luis Vazquez
Departamento de Matematicas
Universidad Autonoma de Madrid
28049 Madrid, Spain
e-mail: juanluis.vazquez@uam.es

Return to the EJDE web page