Electron. J. Diff. Eqns.,
Vol. 2001(2001), No. 64, pp. 1-8.
Stability properties of positive solutions to partial
differential equations with delay
Gyula Farkas & Peter L. Simon
Abstract:
We investigate the stability of positive stationary solutions of
semilinear initial-boundary value problems with delay and convex
or concave nonlinearity. If the nonlinearity is monotone,
then in the convex case
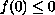 implies instability and in the concave case
implies instability and in the concave case
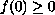 implies stability.
Special cases are shown where the monotonicity assumption can
be weakened or omitted.
implies stability.
Special cases are shown where the monotonicity assumption can
be weakened or omitted.
Submitted June 21, 2001. Published October 8, 2001.
Math Subject Classifications: 35R10, 35B99.
Key Words:
semilinear equations with delay, stability of stationary
solutions, convex nonlinearity, concave nonlineariry.
Show me the
PDF file (212K),
TEX file for this article.
 |
Gyula Farkas
Department of Mathematics
Istvan Szechenyi College
H-9026 Gyor, Hedervariu. 3., Hungary
P{rof. Gyula Farkas died in a traffic accident in Lisbon
on February 27, 2002. |
|---|
 |
Peter L. Simon
School of Chemistry
University of Leeds
Leeds LS2 9JT, UK
e-mail: peters@chem.leeds.ac.uk
|
|---|
Return to the EJDE web page
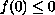 implies instability and in the concave case
implies instability and in the concave case
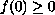 implies stability.
Special cases are shown where the monotonicity assumption can
be weakened or omitted.
implies stability.
Special cases are shown where the monotonicity assumption can
be weakened or omitted.

