Electron. J. Diff. Eqns., Vol. 2001(2001), No. 70, pp. 1-5.
A theorem of Rolewicz's type for measurable
evolution families in Banach spaces
Constantin Buse & Sever S. Dragomir
Abstract:
Let
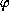 be a positive and non-decreasing function defined on
the real half-line and
be a positive and non-decreasing function defined on
the real half-line and
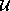 be a strongly measurable,
exponentially bounded evolution family of bounded linear operators
acting on a Banach space and satisfing a certain measurability
condition as in Theorem 1 below.
We prove that if
be a strongly measurable,
exponentially bounded evolution family of bounded linear operators
acting on a Banach space and satisfing a certain measurability
condition as in Theorem 1 below.
We prove that if
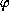 and
and
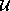 satisfy a certain
integral condition (see the relation \ref{0.1} from Theorem 1 below)
then
satisfy a certain
integral condition (see the relation \ref{0.1} from Theorem 1 below)
then
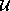 is uniformly exponentially stable. For
is uniformly exponentially stable. For
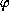 continuous and \mathcal U
strongly continuous and exponentially bounded,
this result is due to Rolewicz. The proofs uses the relatively
recent techniques involving evolution semigroup theory.
continuous and \mathcal U
strongly continuous and exponentially bounded,
this result is due to Rolewicz. The proofs uses the relatively
recent techniques involving evolution semigroup theory.
Submitted September 2, 2001. Published November 23, 2001.
Math Subject Classifications: 47A30, 93D05, 35B35, 35B40, 46A30.
Key Words: Evolution family of bounded linear operators,
evolution operator semigroup, Rolewicz's theorem,
exponential stability.
Show me the
PDF file (215K),
TEX file, and other files for this article.
 |
Constantin Buse
Department of Mathematics
West University of Timisoara
Bd. V. Parvan 4
1900 Timisoara, Romania
e-mail: buse@tim1.math.uvt.ro
|
|---|
 |
Sever S. Dragomir
School of Communications and Informatics
Victoria University of Technology
PO Box 14428
Melburne City MC 8001
Victoria, Australia
e-mail: sever@matilda.vu.edu.au
http://rgmia.vu.edu.au/SSDragomirWeb.html
|
|---|
Return to the EJDE web page
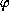 be a positive and non-decreasing function defined on
the real half-line and
be a positive and non-decreasing function defined on
the real half-line and
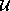 be a strongly measurable,
exponentially bounded evolution family of bounded linear operators
acting on a Banach space and satisfing a certain measurability
condition as in Theorem 1 below.
We prove that if
be a strongly measurable,
exponentially bounded evolution family of bounded linear operators
acting on a Banach space and satisfing a certain measurability
condition as in Theorem 1 below.
We prove that if
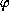 and
and
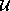 satisfy a certain
integral condition (see the relation \ref{0.1} from Theorem 1 below)
then
satisfy a certain
integral condition (see the relation \ref{0.1} from Theorem 1 below)
then
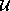 is uniformly exponentially stable. For
is uniformly exponentially stable. For
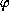 continuous and \mathcal U
strongly continuous and exponentially bounded,
this result is due to Rolewicz. The proofs uses the relatively
recent techniques involving evolution semigroup theory.
continuous and \mathcal U
strongly continuous and exponentially bounded,
this result is due to Rolewicz. The proofs uses the relatively
recent techniques involving evolution semigroup theory.

