We consider a scalar conservation law in the quarter plane. This equation is approximated in a continuous kinetic Bhatnagar-Gross-Krook (BGK) model. The convergence of the model towards the unique entropy solution is established in the space of functions of bounded variation, using kinetic entropy inequalities, without special restriction on the flux nor on the equilibrium problem's data. As an application, we establish the hydrodynamic limit for a
relaxation system with general data. Also we construct a new family
of convergent continuous BGK models with simple maxwellians different
from the
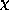models.
