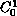 minimizers are also
minimizers are also
 minimizers
minimizers
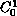 minimizers are also
minimizers are also
 minimizers
minimizers
Yanming Li & Benjin Xuan
Abstract:
Brezis and Niremberg [1] showed that for a certain
functional the
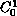 minimizer is also the
minimizer is also the
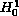 minimizer.
In this paper, we present two functionals for which
a local minimizer in the
minimizer.
In this paper, we present two functionals for which
a local minimizer in the
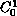 topology is also a local
minimizer in the
topology is also a local
minimizer in the
 topology.
As an application, we show some existence results involving
the sub and super solution method for elliptic equations.
topology.
As an application, we show some existence results involving
the sub and super solution method for elliptic equations.
Submitted November 24, 2001. Published January 24, 2002.
Math Subject Classifications: 35J60.
Key Words:
 minimizers,
minimizers,
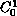 minimizers,
divergence elliptic equation, p-Laplacian.
minimizers,
divergence elliptic equation, p-Laplacian.
Show me the PDF file (297K), TEX file for this article.
| Yanming Li Department of SCGY University of Science and Technology of China Hefei, Anhui 230026, China e-mail: lyqg@mail.ustc.edu.cn | |
 |
Benjin Xuan Department of Mathematics University of Science and Technology of China and Dept. de Matematicas, Universidad Nacional Bogota, Colombia e-mail: wenyuanxbj@yahoo.com |
Return to the EJDE web page