Electron. J. Diff. Eqns., Vol. 2002(2002), No. 11, pp. 1-26.

Blow-up of radially symmetric solutions of a non-local problem modelling Ohmic heating

Dimitrios E. Tzanetis

Abstract:
We consider a non-local initial boundary-value problem for the equation
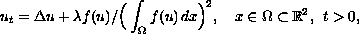
$$ u_t=\Delta u+\lambda f(u)/\Big(\int_{\Omega}f(u)\,dx\Big)^2 ,\quad x \in \Omega \subset \mathbb{R}^2 ,\,\;t>0, $$
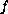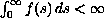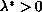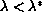where $u$ represents a temperature and $f$ is a positive and decreasing function. It is shown that for the radially symmetric case, if $\int_{0}^{\infty}f(s)\,ds$ less than $\infty $ then there exists a critical value $\lambda^{\ast}$ greater than $0$ such that for $\lambda$ greater than $\lambda^{\ast}$ there is no stationary solution and $u$ blows up, whereas for $\lambda$ less than $\lambda^{\ast}$ there exists at least one stationary solution. 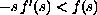Moreover, for the Dirichlet problem with $-s\,f'(s)$ less than $f(s)$ there exists a unique stationary solution which is asymptotically stable. 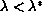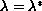For the Robin problem, if $\lambda$ less than $\lambda^{\ast}$ then there are at least two solutions, while if $\lambda=\lambda^{\ast}$ at least one solution. Stability and blow-up of these solutions are examined in this article.

Submitted October 2, 2001. Published February 1, 2002.
Math Subject Classifications: 35B30, 35B40, 35K20, 35K55, 35K99.
Key Words: Nonlocal parabolic equations, blow-up, global existence, steady states.

Show me the PDF file (355K), TEX file, and other files for this article.

Dimitrios E. Tzanetis
Department of Mathematics,
Faculty of Applied Sciences,
National Technical University of Athens,
Zografou Campus, 157 80 Athens, Greece
e-mail: dtzan@math.ntua.gr

Return to the EJDE web page