Electron. J. Diff. Eqns., Vol. 2002(2002), No. 18, pp. 1-16.
Positive and monotone solutions of an m-point boundary value problem
Panos K. Palamides
Abstract:
We study the second-order ordinary differential equation
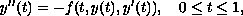
subject to the multi-point boundary conditions
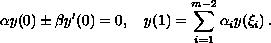
We prove the existence of a positive solution (and monotone in some cases)
under superlinear and/or sublinear growth rate in
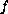 .
Our approach is based
on an analysis of the corresponding vector field on the
.
Our approach is based
on an analysis of the corresponding vector field on the
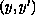 face-plane and on Kneser's property for the solution's funnel.
face-plane and on Kneser's property for the solution's funnel.
Submitted January 10, 2002. Published February 18, 2002.
Math Subject Classifications: 34B10, 34B18, 34B15.
Key Words: multipoint boundary value problems, positive monotone
solution, vector field, sublinear, superlinear,
Kneser's property, solution's funel.
Show me the
PDF file (260K),
TEX file for this article.
 |
Panos K. Palamides
Naval Academy of Greece,
Piraeus 183 03, Greece
and
Department of Mathematics, Univ. of Ioannina,
451 10 Ioannina, Greece
e-mail:ppalam@otenet.gr |
|---|
Return to the EJDE web page
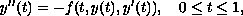
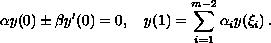
 .
Our approach is based
on an analysis of the corresponding vector field on the
.
Our approach is based
on an analysis of the corresponding vector field on the
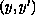 face-plane and on Kneser's property for the solution's funnel.
face-plane and on Kneser's property for the solution's funnel.
