 regularity for nonlinear elliptic systems of second order
regularity for nonlinear elliptic systems of second order
 regularity for nonlinear elliptic systems of second order
regularity for nonlinear elliptic systems of second order
Josef Danecek & Eugen Viszus
Abstract:
This paper is concerned with the regularity of the gradient
of the weak solutions to nonlinear elliptic systems
with linear main parts. It demonstrates the connection between
the regularity of the (generally discontinuous) coefficients
of the linear parts of systems and the regularity of the
gradient of the weak solutions of systems.
More precisely: If above-mentioned coefficients belong
to the class
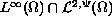 (generalized Campanato spaces),
then the gradient of the weak solutions belong to
(generalized Campanato spaces),
then the gradient of the weak solutions belong to
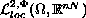 ,
where the relation between the functions
,
where the relation between the functions
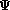 and
and
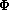 is formulated in Theorems 3.1 and 3.2.
is formulated in Theorems 3.1 and 3.2.
Submitted May 31, 2001. Published February 19, 2002.
Math Subject Classifications: 49N60, 35J60.
Key Words: Nonlinear equations, regularity, Morrey-Campanato spaces.
Show me the PDF file (287K), TEX file for this article.
 |
Josef Danecek Department of Mathematics, Faculty of Civil Engineering, Zizkova 17, 60200 Brno, Czech Republic e-mail: danecek.j@fce.vutbr.cz |
|---|---|
 |
Eugen Viszus Department of Mathematical Analysis, Faculty of Mathematics and Physics, Comenius University, Mlynska dolina, 84248 Bratislava, Slovak Republic e-mail: Eugen.Viszus@fmph.uniba.sk |
Return to the EJDE web page