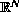 with an indefinite functional
with an indefinite functional
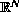 with an indefinite functional
with an indefinite functional
David G. Costa, Yuxia Guo, & Miguel Ramos
Abstract:
We prove the existence of a nontrivial solution for the nonlinear
elliptic problem
 in
in
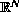
where
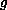 is superlinear near zero and near infinity,
is superlinear near zero and near infinity,
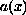 changes sign,
changes sign,
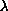 is positive, and
is positive, and
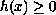 is a weight function. For
is a weight function. For
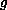 odd, we prove the
existence of an infinite number of solutions.
odd, we prove the
existence of an infinite number of solutions.
Submitted June 23, 2001. Published March 4, 2002.
Math Subject Classifications: 35J25, 35J20, 58E05.
Key Words: Superlinear elliptic problems, Morse index, minimax methods.
Show me the PDF file (298K), TEX file for this article.
Yuxia Guo
Chinese Academy of Sciences
Beijing 100080, China
e-mail: yxguo@lsc02.iss.ac.cn
Miguel Ramos
CMAF, Univ. de Lisboa
Av. Prof. Gama Pinto,
1649-003 Lisboa, Portugal
e-mail: mramos@lmc.fc.ul.pt