Electron. J. Diff. Eqns., Vol. 2002(2002), No. 28, pp. 1-10.
Oscillation criteria for a class of nonlinear partial differential
equations
Robert Marik
Abstract:
This paper presents sufficient conditions on the function
 to ensure that every solution of partial differential equation
to ensure that every solution of partial differential equation
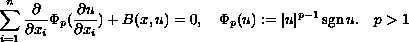
is weakly oscillatory, i.e. has zero outside of every ball in
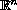 .
The main tool is modified Riccati technique
developed for Schrodinger operator by Noussair and Swanson [11].
.
The main tool is modified Riccati technique
developed for Schrodinger operator by Noussair and Swanson [11].
Submitted May 24, 2001. Published March 8, 2002.
Math Subject Classifications: 35B05
Key Words: Oscillation criteria, nonlinear oscillation, unbounded domains.
Show me the
PDF file (242K),
TEX file for this article.
 |
Robert Marik
Dept. of Mathematics, Mendel University
Zemedelska 3
613 00 Brno, Czech Republic
e-mail: marik@mendelu.cz |
|---|
Return to the EJDE web page
 to ensure that every solution of partial differential equation
to ensure that every solution of partial differential equation
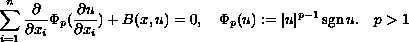
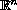 .
The main tool is modified Riccati technique
developed for Schrodinger operator by Noussair and Swanson [11].
.
The main tool is modified Riccati technique
developed for Schrodinger operator by Noussair and Swanson [11].
