In this paper we study the stability of the single internal spike solution of the shadow system for the Gierer-Meinhardt equations in one space dimension. It is well-known, that the linearization around this spike consists of a differential operator plus a non-local term. For parameter values in certain subsets of the 3D
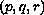 -parameter
space we
prove that the non-local term moves the negative
-parameter
space we
prove that the non-local term moves the negative
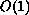 eigenvalue
of the differential operator to the positive (stable) half plane
and that an exponentially small
eigenvalue remains in the negative half plane, indicating a
marginal instability (dubbed ``metastability''). We also
show, that for parameters
eigenvalue
of the differential operator to the positive (stable) half plane
and that an exponentially small
eigenvalue remains in the negative half plane, indicating a
marginal instability (dubbed ``metastability''). We also
show, that for parameters
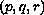 in another region, the
in another region, the
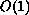 eigenvalue remains in the negative half plane.
In all asymptotic approximations we compute
rigorous bounds for the order of the error.
eigenvalue remains in the negative half plane.
In all asymptotic approximations we compute
rigorous bounds for the order of the error.

