Electron. J. Diff. Eqns., Vol. 2002(2002), No. 61, pp. 1-10.
Existence of solutions for discontinuous functional equations
and elliptic boundary-value problems
Siegfried Carl & Seppo Heikkila
Abstract:
We prove existence results for discontinuous functional equations
in general
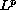 -spaces
and apply these results to the solvability of
implicit and explicit elliptic boundary-value problems involving
discontinuous nonlinearities. The main tool in the proof is a
fixed point result in lattice-ordered Banach spaces proved by the
second author.
-spaces
and apply these results to the solvability of
implicit and explicit elliptic boundary-value problems involving
discontinuous nonlinearities. The main tool in the proof is a
fixed point result in lattice-ordered Banach spaces proved by the
second author.
Submitted January 15, 2002. Published June 25, 2002.
Math Subject Classifications: 35J65, 35R05, 35R10.
Key Words: functional equations, elliptic boundary-value problems,
discontinuous nonlinearities.
Show me the
PDF file (227K),
TEX file for this article.
Siegfried Carl
Current address:
Florida Institute of Technology,
Department of Mathematical Sciences,
150 West University Boulevard,
Melbourne, FL 32901, USA,
e-mail: scarl@fit.edu
permanent address:
Martin-Luther-Universitat Halle-Wittenberg,
Fachbereich Mathematik und Informatik,
Institut fur Analysis,
06099 Halle, Germany
email: carl@mathematik.uni-halle.de
Seppo Heikkila
Department of Mathematical Sciences, University of Oulu,
Box 3000, FIN-90014,
University of Oulu, Finland
Fax: 358 8 5531730.
e-mail: sheikki@cc.oulu.fi
Return to the EJDE web page
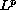 -spaces
and apply these results to the solvability of
implicit and explicit elliptic boundary-value problems involving
discontinuous nonlinearities. The main tool in the proof is a
fixed point result in lattice-ordered Banach spaces proved by the
second author.
-spaces
and apply these results to the solvability of
implicit and explicit elliptic boundary-value problems involving
discontinuous nonlinearities. The main tool in the proof is a
fixed point result in lattice-ordered Banach spaces proved by the
second author.