Most publications on reaction-diffusion systems of
 components
(
components
(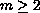 )
impose
)
impose
 inequalities to the reaction terms,
to prove existence of global solutions
(see Martin and Pierre [10] and Hollis [4]).
The purpose of this paper is to prove existence of a global solution
using only one inequality in the case of 3 component systems.
Our technique is based on the construction of polynomial functionals
(according to solutions of the reaction-diffusion equations)
which give, using the well known regularizing effect,
the global existence. This result generalizes those obtained
recently by Kouachi [6] and independently by Malham
and Xin [9].
inequalities to the reaction terms,
to prove existence of global solutions
(see Martin and Pierre [10] and Hollis [4]).
The purpose of this paper is to prove existence of a global solution
using only one inequality in the case of 3 component systems.
Our technique is based on the construction of polynomial functionals
(according to solutions of the reaction-diffusion equations)
which give, using the well known regularizing effect,
the global existence. This result generalizes those obtained
recently by Kouachi [6] and independently by Malham
and Xin [9].
