We study the phase space of the evolution equation

where
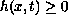 .
The parameters
.
The parameters
 ,
,
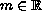 ,
and the Bond number
,
and the Bond number
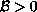 are given.
We find numerically, for some ranges of
are given.
We find numerically, for some ranges of
 and
and
 , that
perturbing the positive periodic steady state in a certain direction
yields a solution that relaxes to the constant steady state. Meanwhile
perturbing in the opposite direction yields a solution that appears to
touch down or `rupture' in finite time, apparently approaching a
compactly supported `droplet' steady state.
We then investigate the structural stability of the evolution by
changing the mobility coefficients,
, that
perturbing the positive periodic steady state in a certain direction
yields a solution that relaxes to the constant steady state. Meanwhile
perturbing in the opposite direction yields a solution that appears to
touch down or `rupture' in finite time, apparently approaching a
compactly supported `droplet' steady state.
We then investigate the structural stability of the evolution by
changing the mobility coefficients,
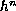 and
and
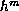 .
We find evidence
that the above heteroclinic orbits between steady states are perturbed
but not broken, when the mobilities are suitably changed.
We also investigate touch-down singularities, in which the solution
changes from being everywhere positive to being zero at isolated
points in space. We find that changes in the mobility exponent
.
We find evidence
that the above heteroclinic orbits between steady states are perturbed
but not broken, when the mobilities are suitably changed.
We also investigate touch-down singularities, in which the solution
changes from being everywhere positive to being zero at isolated
points in space. We find that changes in the mobility exponent
 can affect the number of touch-down points per period,
and affect whether these singularities occur in finite or infinite time.
can affect the number of touch-down points per period,
and affect whether these singularities occur in finite or infinite time.
