Electron. J. Diff. Eqns., Vol. 2002(2002), No. 99, pp. 1-20.

A note on a Liouville-type result for a system of fourth-order equations in $\mathbb{R}^N$

Ana Rute Domingos & Yuxia Guo

Abstract:
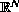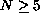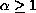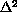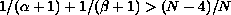We consider the fourth order system $\Delta^2 u =v^\alpha,\Delta^2 v =u^\beta$ in $\mathbb{R}^N$, for $N\geq 5$, with $\alpha\geq 1$, $\beta\geq 1$, where $\Delta^2$ is the bilaplacian operator. For $1/(\alpha +1) +1/(\beta +1)$ greater than $(N-4)/N$ we prove the non-existence of non-negative, radial, smooth solutions. For $\alpha,\beta\leq (N+4)/(N-4)$ we show the non-existence of non-negative smooth solutions.

Submitted November 27, 2001. Published November 27, 2002.
Math Subject Classifications: 35J60.
Key Words: Elliptic system of fourth order equations, moving-planes.

Show me the PDF file (271K), TEX file, and other files for this article.

Ana Rute Domingos
CMAF, Universidade de Lisboa
Av. Prof. Gama Pinto, 2
P-1649-003 Lisboa, Portugal
e-mail: rute@ptmat.ptmat.fc.ul.pt
Yuxia Guo
Department of Mathematics
Tsinghua University
Beijing, 100084, China
e-mail: yxguo@yahoo.com

Return to the EJDE web page