In 1952, at a conference in New York, Protter formulated some boundary value problems for the wave equation, which are three-dimensional analogues of the Darboux problems (or Cauchy-Goursat problems) on the plane. Protter studied these problems in a 3-D domain
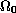 ,
bounded by two characteristic cones
,
bounded by two characteristic cones
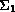 and
and
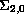 ,
and by a plane region
,
and by a plane region
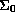 .
It is well known that, for an infinite number of smooth functions
in the right-hand side, these problems do not have classical solutions.
Popivanov and Schneider (1995) discovered the reason of this fact for the
case of Dirichlet's and Neumann's conditions on
.
It is well known that, for an infinite number of smooth functions
in the right-hand side, these problems do not have classical solutions.
Popivanov and Schneider (1995) discovered the reason of this fact for the
case of Dirichlet's and Neumann's conditions on
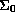 :
the strong
power-type singularity appears in the generalized solution on the
characteristic cone
:
the strong
power-type singularity appears in the generalized solution on the
characteristic cone
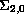 .
In the present paper we consider the
case of third boundary-value problem on
.
In the present paper we consider the
case of third boundary-value problem on
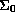 and obtain the
existence of many singular solutions for the wave equation involving
lower order terms. Especifically, for Protter's problems in
and obtain the
existence of many singular solutions for the wave equation involving
lower order terms. Especifically, for Protter's problems in
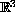 it is shown here that for any
it is shown here that for any
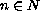 there exists a
there exists a
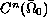 -function, for which the corresponding unique
generalized solution belongs to
-function, for which the corresponding unique
generalized solution belongs to
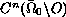 and has a strong power type singularity at the point
and has a strong power type singularity at the point
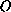 .
This singularity is isolated at the vertex
.
This singularity is isolated at the vertex
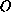 of the characteristic cone
of the characteristic cone
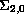 .
and does not propagate along the cone. For the
wave equation without lower order terms, we presented the exact behavior of
the singular solutions at the point
.
and does not propagate along the cone. For the
wave equation without lower order terms, we presented the exact behavior of
the singular solutions at the point
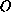 .
.


